In meinen früheren Blogs habe ich verschiedene konstitutive Modelle für die Modellierung des Spannungs-Dehnungs-Verhaltens von Böden und Felsen erörtert. Es ist wichtig, ein fortschrittliches konstitutives Modell zu verwenden, das alle relevanten Merkmale des Boden- oder Gesteinsverhaltens im Hinblick auf die Art des Bodens oder des Gesteins und die Bedingungen, die sich aus der Anwendung ergeben, berücksichtigt. Die entsprechenden Modellparameter werden idealerweise aus ausreichenden Daten der Baugrunduntersuchung ermittelt. PLAXIS bietet komfortable Möglichkeiten, um den Anwender bei der Ermittlung geeigneter Parameterwerte zu unterstützen.
Geotechnische Anwendungen beinhalten oft Bauwerke und andere Objekte, die mit dem umgebenden Boden interagieren. Obwohl das Verhalten des Bodens im Allgemeinen kritischer und komplexer ist als das von eingebetteten Bauwerken, ist es wichtig, dass Bauwerke mit der gleichen Genauigkeit modelliert werden wie der Boden. Neben speziellen Strukturelementen und Schnittstellen für die Boden-Bauwerk-Interaktion enthält PLAXIS spezielle konstitutive Modelle, um die Standardvolumenelemente für die Modellierung von Strukturmaterialvolumen zu verwenden. Um konkret zu sein, werde ich in diesem Blog auf die konstitutiven Modelle für Beton und Mauerwerk eingehen.
Beton-Modell
Beton ist ein bekannter Werkstoff im Bauwesen und in der Geotechnik. Fundamente, Wände, Kellergeschosse und Tunnelauskleidungen werden meist aus Beton hergestellt. Beton ist viel steifer und fester als Boden, so dass er in vielen geotechnischen Anwendungen als linear elastisches Material angesehen werden kann. Um jedoch die Bemessung von (unbewehrten) Betonstrukturen, die in den Boden eingebettet sind, zu optimieren, muss der Beton als ein nichtlineares und zeitabhängiges Material modelliert werden. Ausgehend von einem Modell für Spritzbeton-Tunnelauskleidungen (Schädlich & Schweiger, 2014) beinhaltet das Betonmodell mehrere Merkmale des Betonverhaltens, die im linear-elastischen Modell nicht enthalten sind:
- Das elastische Steifigkeitsverhalten, das eine kurzfristige Aushärtung von jungem Beton ermöglicht.
- Die Materialfestigkeit erlaubt auch eine kurzfristige Aushärtung
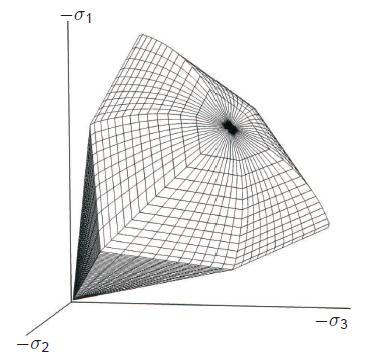
- Mohr-Coulomb-Verfestigung/Erweichung und Versagenskriterium in Druck und Scherung
- Rankine-Versagenskriterium und Dehnungserweichung in Zug
- Regularisierung des Erweichungsverhaltens, um die Netzabhängigkeit der Ergebnisse zu verringern
- Zeitabhängiges viskoelastisches Kriechverhalten auf lange Sicht
- Spannungsunabhängiges Schwindverhalten
Die Verwendung des Betonmodells in PLAXIS führt zu einer realistischeren Spannungsverteilung in dicken (unbewehrten) Betondecken, Wänden oder Tunnelauskleidungen. Die Spannungsspitzen an Kanten und Ecken sind aufgrund der plastischen Verformung im Allgemeinen geringer als bei Verwendung des linear-elastischen Modells. Wenn Ihre Betonstruktur keine hohen Spitzenspannungen enthalten darf, können Sie das Betonmodell verwenden, um eine realistischere Spannungsverteilung zu erhalten.
Modell des Mauerwerks
Die Bauweise, bei der Ziegel in einem regelmäßigen Muster gemauert und mit Mörtel verbunden werden, ist sehr alt. Zur Zeit des Römischen Reiches wurden viele Gebäude, Brücken und Aquädukte aus Mauerwerk gebaut; einige davon sind noch heute erhalten, einige sind sogar 2000 Jahre alt.
Neben Brücken und Aquädukten wurde Mauerwerk auch im Geo- und Wasserbau für den Bau von Kaimauern und Bodenverbauungen verwendet. Obwohl die meisten dieser Bauwerke heute aus Beton gebaut werden, können für die Stabilitätsbewertung und die Nachrüstung bestehender Mauerwerksbauten Finite-Elemente-Berechnungen durchgeführt werden, bei denen das Mauerwerk genau modelliert wird. Eine weitere Anwendung sind dynamische Erdbebensimulationen zur Analyse der Auswirkungen von Erdbeben auf Mauerwerksbauten.
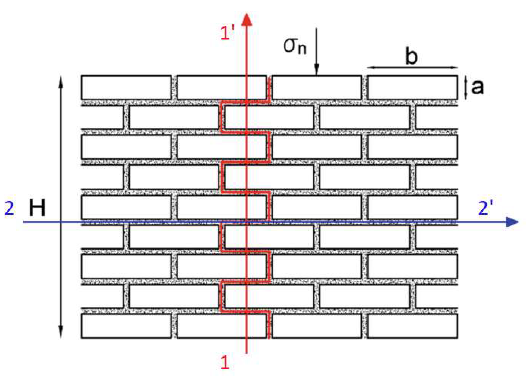
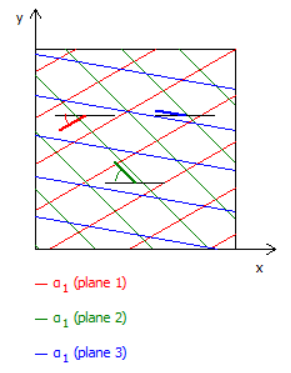
PLAXIS verfügt über ein benutzerdefiniertes Modell für die Modellierung von Mauerwerksbauten. Dieses Modell wurde in Zusammenarbeit mit der Universität Sapienza in Rom entwickelt (Amorosi et al., 2014; Lasciarrea et al. 2019). Das Masonry-Modell beinhaltet eine anisotrope Festigkeit mit vordefinierten Versagensrichtungen, die auf dem typischen Muster und der Struktur der Ziegelsteine basieren. Das Masonry-Modell basiert auf dem Jointed-Rock-Modell (siehe vorheriger Blog über Gesteinsmodelle). Die Abbildung zeigt die charakteristischen Versagensmechanismen entlang der Kopffugen (1-1') und der Lagerfugen (2-2'), die im Modell berücksichtigt werden. Die Parameter der Coulombschen Scherfestigkeit und der Zugfestigkeit in den verschiedenen Versagensrichtungen hängen von den mechanischen Eigenschaften von Ziegel und Mörtel sowie von den geometrischen Eigenschaften der Ziegel a und b ab.

Abbildung 1. Charakteristische Versagensmechanismen in einem Mauerwerksbauwerk
Statische Modellierung als Teil Ihrer geotechnischen Analyse
Obwohl PLAXIS nicht für die Tragwerksplanung gedacht ist, enthält es spezielle Strukturelemente und konstitutive Modelle zur Simulation von Strukturobjekten und deren Interaktion mit dem umgebenden Boden. Diese Modelle ermöglichen eine genaue Berechnung von strukturellen Spannungen, Kräften, Verformungen und Mechanismen als Teil Ihrer geotechnischen Analyse. Die folgenden Modelle wurden in diesem Blog besprochen:
- Das Betonmodell ist ein nichtlineares und zeitabhängiges konstitutives Modell zur Simulation des Verhaltens von im Boden eingebetteten (unbewehrten) Betonstrukturen.
- Das Mauerwerksmodell ist ein lineares, elastisches, perfekt plastisches Modell mit vorherrschenden Anisotropierichtungen, die den charakteristischen Versagensmechanismen von Mauerwerk entsprechen.
Wenn Ihr Projekt solche Baumaterialien umfasst, zögern Sie nicht, die oben genannten Modelle zu verwenden und die Möglichkeiten der Strukturmodellierung in PLAXIS als Teil Ihrer geotechnischen Finite-Elemente-Analyse zu entdecken.
Text by Dr. Ronald B.J. Brinkgreve, Bentley Systems, 24.03.2021
References:
1. Schädlich B, Schweiger HF (2014). A new constitutive model for shotcrete. In: Numerical Methods in Geotechnical Engineering – Hicks, Brinkgreve & Rohe (Eds). Leiden: CRC press. 103-108.
2. Amorosi, A., Boldini, D., de Felice, G., Malena, M., Di Mucci, G. (2014). Numerical modelling of the interaction between a deep excavation and an ancient masonry wall. In: Geotechnical Aspects of Underground Construction in Soft Ground – Yoo, Park, Kim & Ban (Eds). Seoul: Korean Geotechnical Society.
3. Lasciarrea WG, Amorosi A, Boldini D, de Felice G, Malena M (2019). Jointed Masonry Model: a constitutive law for 3D soil-structure interaction analysis. Engineering Structures, 201.