Obwohl PLAXIS seine Wurzeln in weichen Böden hat, ist es für Finite-Elemente-Analysen in harten Böden und Felsen gut ausgestattet. Zusätzlich zu den speziellen Funktionen für die Modellierung von Tunneln, Felsbolzen und Feldspannungsbedingungen enthält es die erforderlichen konstitutiven Modelle zur Simulation des Verhaltens verschiedener Felsarten.
Merkmale des Felsverhaltens
In dieser Reihe von Blogs über konstitutive Modelle habe ich oft die "Merkmale des Bodenverhaltens" erwähnt. Da wir hier über Gestein sprechen, möchte ich nun einige "Merkmale des Gesteinsverhaltens" erwähnen und auf die Unterschiede zum Bodenverhalten hinweisen:
- Die Steifigkeit des Gesteins ist deutlich höher als die des Bodens und kaum spannungsabhängig.
- Die Festigkeit des Gesteins ist deutlich höher als die des Bodens, vor allem der kohäsive Teil der Festigkeit, und sie steigt weniger als linear mit dem Spannungsniveau.
- Das Gesteinsverhalten ist häufig anisotrop, sowohl in Bezug auf die Steifigkeit als auch auf die Festigkeit; es wird in hohem Maße durch die geologische Vorgeschichte beeinflusst, die zu Abnutzung (Verwitterung), Klüften, Rissen, Fugen, Verwerfungen und anderen Unregelmäßigkeiten oder Diskontinuitäten geführt haben kann.
- Gesteinsverformungen können zeitabhängig sein (Kriechen), unterscheiden sich jedoch stark vom Kriechen in weichen Böden.
Es ist zu beachten, dass das Gesteinsverhalten (selbst bei ein und derselben Gesteinsformation) aufgrund lokaler Unregelmäßigkeiten von einem Ort zum anderen sehr unterschiedlich sein kann. Wenn eine (intakte) Gesteinskernprobe entnommen und im Labor untersucht wird, sind die gemessenen Eigenschaften im Allgemeinen günstiger als die der Gesteinsmasse. Daher ist eine Felduntersuchung zur Bestimmung repräsentativer Gesteinseigenschaften erforderlich.
Hoek-Brown-Modell
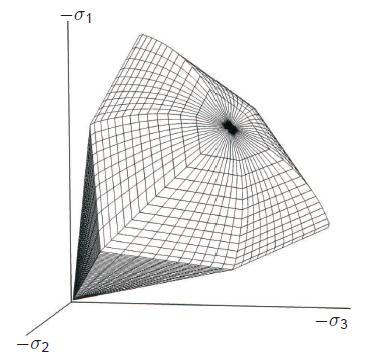
Das Hoek-Brown-Modell ist eine Kombination aus dem Hooke'schen Elastizitätsgesetz und dem Hoek-Brown-Versagenskriterium. Dieses bekannte Versagenskriterium für Gestein drückt aus, dass die Festigkeit des Gesteins weniger als linear mit dem Spannungsniveau zunimmt. Das Hoek-Brown-Modell ist in erster Linie für verwittertes Gestein gedacht. In PLAXIS gibt es ein praktisches Verfahren zur Bestimmung der fünf Modellparameter auf der Grundlage von Felduntersuchungen, Labortestdaten und empirischen Daten.
Das Hoek-Brown-Standardmodell in PLAXIS ist linear elastisch und perfekt plastisch. Es gibt eine erweiterte Version des Hoek-Brown-Modells als benutzerdefiniertes Modell mit zusätzlicher Eingabe von Parametern für Zugfestigkeit und Restfestigkeit (Marinelli et al., 2018). Dieses Modell wird als "Hoek & Brown-Modell mit Erweichung" bezeichnet und umfasst das Erweichungsverhalten, d. h. die Verringerung der Festigkeit durch plastische Dehnung, bis die Restfestigkeit erreicht ist.
Modell für gefügtes Gestein
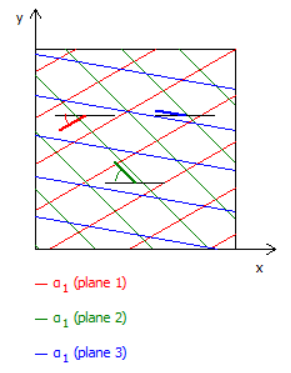
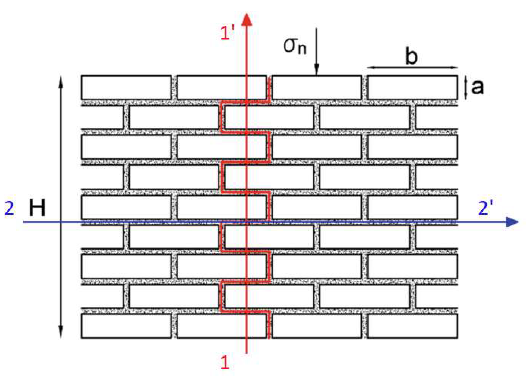
Das Hoek-Brown-Modell kann nicht explizit mit diskreten Systemen von Fugen und Brüchen umgehen, die ein erhebliches anisotropes Verhalten in der Gesteinsmasse hervorrufen könnten. Wenn Ihr Projekt ein Gestein mit gut definierten Diskontinuitäten umfasst, ist das Modell für geklüftetes Gestein für dieses Gestein besser geeignet. Die Schichtungsrichtung (und andere vorherrschende Versagensrichtungen) kann mit den Parametern "Neigung" und "Streichen" modelliert werden.

Abbildung: Beispiel mit drei verschiedenen Eintauchwinkeln, definiert durch den Parameter
Das Standardmodell von Jointed-Rock in PLAXIS ist linear-elastisch und vollkommen plastisch. Plastische Verformung kann nur in den vordefinierten Bruchrichtungen auftreten. Dies bedeutet, dass die Gesteinsmatrix als linear elastisch betrachtet wird (unbegrenzte Scherfestigkeit), was als Einschränkung angesehen werden kann. Für den Fall, dass Sie die Gesteinsmatrix als elastoplastisches Material definieren möchten, steht Ihnen ein benutzerdefiniertes Modell zur Verfügung, das diese Möglichkeit bietet, nämlich das Modell "Isotropic Jointed Rock with Mohr-Coulomb Failure Criterion".
N2PC Steinsalz-Modell
Neben den Standard-Felsmodellen in PLAXIS gibt es eine Reihe von benutzerdefinierten Modellen, die spezielle Gesteinsmerkmale enthalten. Das N2PC-Steinsalzmodell, ein Norton-Based Double Power Creep Model (Bui et al., 2018), ist ein Modell, das für Salzgestein und andere Gesteinsarten mit zeitabhängigem Kriechverhalten gedacht ist. Es kann für tiefe unterirdische Projekte im Bergbau und in der Erdölindustrie wie Energiespeicherung und Gasförderung verwendet werden. In Kombination mit den eingebauten thermischen Fähigkeiten in PLAXIS 2D Ultimate kann das Kriechen im N2PC Steinsalzmodell sogar als temperaturabhängig definiert werden.
Modell für quellendes Gestein
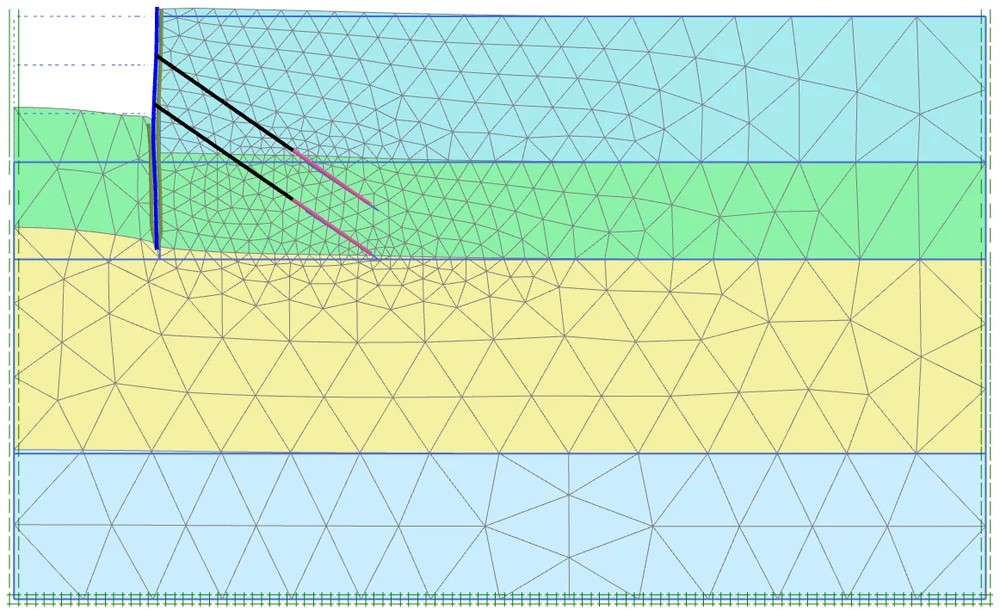
Das Modell für quellendes Gestein (Schädlich et al. 2013) ist ein weiteres benutzerdefiniertes Modell, das eine spezielle Gesteinsfunktion enthält: Quellung. Ein typisches Beispiel für die Anwendung dieses Modells ist ein Tunnelprojekt in Anhydritgestein. Wenn der Anhydrit mit Wasser in Berührung kommt, kann er mit der Zeit um bis zu 60 % anschwellen. Dies kann zu erheblichen zusätzlichen Spannungen oder Verformungen in der Tunnelauskleidung führen. Mit dem Modell Quellgestein und den Möglichkeiten der Tunnelmodellierung ist PLAXIS gut gerüstet, um solche Analysen durchzuführen.
Starten Sie noch heute Ihre Felsanalyse mit PLAXIS
Wie Sie in diesem Blog gesehen haben, verfügt PLAXIS nicht nur über Möglichkeiten zur geotechnischen Analyse von (weichen) Böden, sondern auch über die Fähigkeit, genaue Finite-Elemente-Berechnungen für komplexe Projekte im Fels durchzuführen. Der effiziente Arbeitsablauf in Kombination mit den robusten konstitutiven Modellen macht PLAXIS zum idealen Werkzeug für Projekte, die Felsstabilität, Tunnel, tiefe unterirdische (Energie-)Speicher und vieles mehr betreffen. Beginnen Sie also noch heute mit Ihrer Felsanalyse mit PLAXIS und Sie werden feststellen, dass PLAXIS für Fels ebenso gut geeignet ist wie für Boden.
Engl. Original-Text by Dr. Ronald B.J. Brinkgreve, Bentley Systems, 17.03.2021
References
Bui TA, Brinkgreve RBJ, Zampich L (2018). The Norton-Based Double Power Creep Model for Rock Salt. N2PC User Manual. Delft: Plaxis bv.
Marinelli F, Zalamea N, Brasile S, Brinkgreve RBJ (2019). An Advanced Hoek & Brown Model with Softening. User Manual. Delft: Plaxis bv.
Schädlich B, Schweiger HF, Marcher T (2013). Numerical Analysis of Swelling Deformations in Tunnelling – A Case Study. Proceedings EURO:TUN 2013, 3rd Int. Conf. on Computational Methods in Tunnelling and Subsurface Engineering (ed. G. Meschke). Aedificatio Publishers, 429-436.